Understanding the coupling of cranial blood flow and the cerebrospinal fluid system: an in vivo and in silico study
Contents
Team
The problem
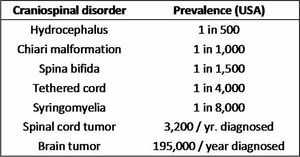
It has been postulated that pathological coupling between cranial blood flow (CBF) and cerebrospinal fluid (CSF) pulsations (Madsen, Egnor et al. 2006; Luciano and Dombrowski 2007) is an important factor influencing the disease pathogenesis of various craniospinal disorders including hydrocephalus, spina bifida, Chiari malformation and syringomyelia, tethered cord, tumors of the spinal cord and brain, and others (Table 1). Coupling of CBF and the CSF system has also been hypothesized to be important in cerebrovascular disorders including Alzheimer’s disease, vascular dementia, stroke, angiogenesis, cerebral ischemia and hyperemia, intracranial hemorrhage, among many others. To understand the complex factors governing CBF and CSF transport a number of in silico studies have been performed in conjunction with in vivo measurements. These studies can be divided into two major groups, those which focus primarily on fluid dynamics (Ursino and Lodi 1997; Cebral, Castro et al. 2003) and those which focus on cerebral autoregulation (Banaji, Tachtsidis et al. 2005).
While the past studies have provided insights into CBF and CSF regulation, there is paucity in studies focusing on how intracranial pressure (ICP) influences cerebral hemodynamics and autoregulation (David and Moore 2008). At present, understanding of the influence of CSF motion on CBF remains in infancy. Thus, the computational models have had limited application in clinical settings where, in many cases, the influence of CSF hydrodynamics is thought to have a strong impact.
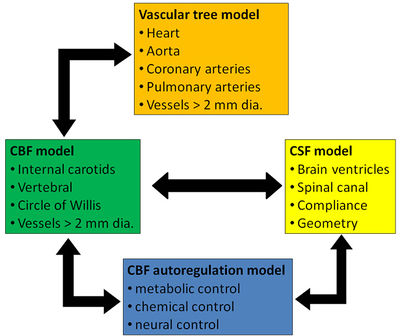
The proposed study will provide a hydrodynamic CBF model which couples with the CSF system by accounting for important CSF system factors such as CSF pulsatility and changes in spinal canal compliance and geometry. Our groups expertise in vascular blood flow modeling (Stergiopulos, Young et al. 1992; Reymond, Merenda et al. 2009), CSF hydrodynamics (Martin, Kalata et al. 2005; Kalata, Martin et al. 2009; Martin, Labuda et al. 2009), and constitutive modeling of vessels (Rachev, Stergiopulos et al. 1998), is well suited for the task. The proposed model can account for CBF autoregulation (Figure 1) by connecting it with existing models which include metabolic control, chemical control, and neural control in a similar manner as braincirc1.0 by Bajani et al. (Banaji, Tachtsidis et al. 2005). The proposed model will also account for changes in vascular blood flow, compliance, and peripheral resistance by coupling with our group’s complete vascular tree model (Reymond, Merenda et al. 2009) (Figure 1).
Hypothesis and research objectives
We hypothesize that CBF and CSF have a coupling effect which plays a role in the biomechanical mechanisms responsible for craniospinal pathologies. The goal of this research is thus to design, develop, and analyze a coupled CBF and CSF in silico model and prove the efficacy of the model through comparison to in vivo and in vitro measurements.
Methods and study outline
The work plan will comprise the following phases:
- A. In vivo measurements.
Our approach is to obtain detailed in vivo measurements on a healthy human subject pertaining to CBF and CSF pulsations which will be used to guide the in silico model development. The following measurements will be obtained:
Phase contrast MR flow measurements (pcMR)
- Craniospinal compliance by CSF pressure wave phase speed (Kalata, Martin et al. 2009)
- Craniospinal compliance by localized volumetric compensation (Martin, Kalata et al. 2005)
- CSF flow and pulsatility at the craniospinal junction (C2) (Loth, Yardimci et al. 2001; Martin, Kalata et al. 2005)
- Vertebral artery, internal carotid artery, and jugular vein flow (total CBF) (Alperin, Lee et al. 2000)
- Anterior and posterior spinal artery flow
MR measurements (geometric)
- High resolution cerebrovascular scan (Reymond, Merenda et al. 2009)
- High resolution CSF scan (brain and spinal canal) (Loth, Yardimci et al. 2001; Martin, Kalata et al. 2005)
- B. In silico model development and testing.
The detailed in vivo MR and US measurements will be used to construct the coupled CBF and CSF in silico model. This model will take into account important properties of the CSF system including local changes in compliance, geometry, and flow pulsatility. The model will be tuned to accurately reflect the single healthy subject’s in vivo measurements.
Expected results and potential impact
The proposed in vivo measurements and in silico model addresses a significant gap in the fundamental understanding the coupling between the CBF and CSF system. The in vivo measurements will provide detailed geometric and flow conditions for the proposed study and other studies interested in CBF autoregulation. The in silico model will serve as a platform for future development and linking with comprehensive models of CBF autoregulation. If proven efficacious, the in silico model, which takes into account the entire vascular tree and CSF system, has the potential to provide a clinically useful tool for interpretation of bedside tests related to cerebral perfusion and CSF system function.
Preliminary results
To be posted
References
Alperin, N. J., S. H. Lee, et al. (2000). "MR-Intracranial pressure (ICP): a method to measure intracranial elastance and pressure noninvasively by means of MR imaging: baboon and human study." Radiology 217(3): 877-85. Banaji, M., I. Tachtsidis, et al. (2005). "A physiological model of cerebral blood flow control." Math Biosci 194(2): 125-73. Cebral, J. R., M. A. Castro, et al. (2003). "Blood-flow models of the circle of Willis from magnetic resonance data." Journal of Engineering Mathematics 47(3-4): 369-386.
David, T. and S. Moore (2008). "Modeling perfusion in the cerebral vasculature." Med Eng Phys 30(10): 1227-45.
Kalata, W., B. Martin, et al. (2009). "MR Measurement of Cerebrospinal Fluid Velocity Wave Speed in the Spinal Canal." IEEE Trans Biomed Eng.
Loth, F., M. A. Yardimci, et al. (2001). "Hydrodynamic modeling of cerebrospinal fluid motion within the spinal cavity." J Biomech Eng 123(1): 71-9.
Luciano, M. and S. Dombrowski (2007). "Hydrocephalus and the heart: interactions of the first and third circulations." Cleve Clin J Med 74 Suppl 1: S128-31.
Madsen, J. R., M. Egnor, et al. (2006). "Cerebrospinal fluid pulsatility and hydrocephalus: the fourth circulation." Clin Neurosurg 53: 48-52.
Martin, B. A., W. Kalata, et al. (2005). "Syringomyelia hydrodynamics: an in vitro study based on in vivo measurements." J Biomech Eng 127(7): 1110-20.
Martin, B. A., R. Labuda, et al. (2009). "Spinal Canal Pressure Measurements in an In Vitro Spinal Stenosis Model: Implications on Syringomyelia Theories." J Biomech Eng In Press(June 2009).
Rachev, A., N. Stergiopulos, et al. (1998). "A model for geometric and mechanical adaptation of arteries to sustained hypertension." J Biomech Eng 120(1): 9-17.
Reymond, P., F. Merenda, et al. (2009). "Validation of a one-dimensional model of the systemic arterial tree." Am J Physiol Heart Circ Physiol 297(1): H208-22.
Stergiopulos, N., D. F. Young, et al. (1992). "Computer simulation of arterial flow with applications to arterial and aortic stenoses." J Biomech 25(12): 1477-88.
Ursino, M. and C. A. Lodi (1997). "A simple mathematical model of the interaction between intracranial pressure and cerebral hemodynamics." Journal of Applied Physiology 82(4): 1256-1269.